Quick Facts
Photo of me:

M.S. Mechanical Engineering (Dec 2022)
-Computational Nuclear Engineering
-4.0 Grad GPA
B.S. Mechanical Engineering (May 2020)
-CS Minor (Pursuing)
-Business Minor
-3.73 Major GPA
Projects
A few of my passion and school projects
SENIOR DESIGN PROJECT
Transient Power Generation for a Gravitional Energy Storage Device
Overview
The proliferation of solar and wind power has created a growing demand for energy storage. My senior design team was tasked with creating a gravitational energy storage device to meet this need in a safe and environmentally friendly way. The scope of the project ranged from concept generation to small-scale prototyping. This webpage, however, focuses exclusively on the model I created that simulates the physical operation and transient power generation of our device. I found this part of the project to be particularly fascinating because of how many different classes I needed to apply to find a solution.
Methodology
Create Free Body Diagrams
Determine Equations of Motion
Develop Differential Equations
Compute Numerical Solution in MATLAB
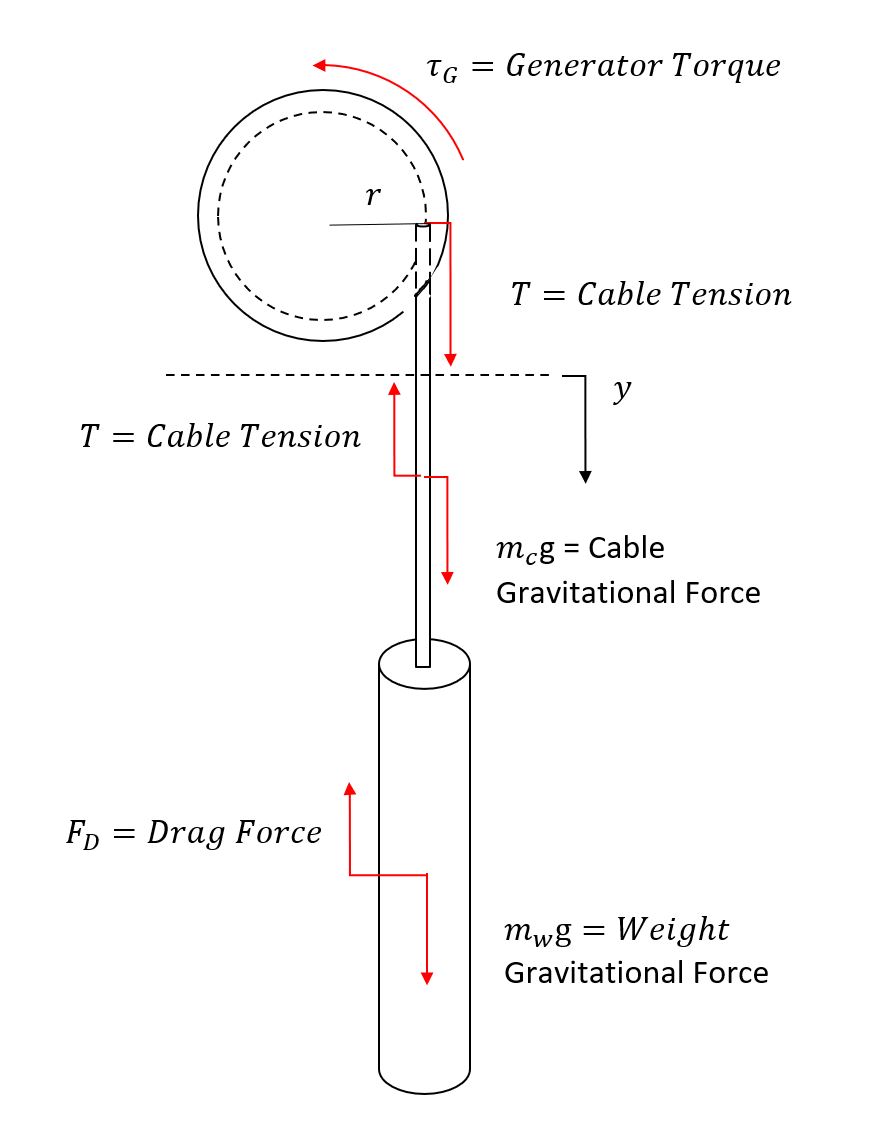
Free Body Diagram
A hanging weight is connected to a spool by a steel cable. The weight, spool, and cable each have their own mass. An electric generator is attached to the spool which converts the mechanical energy of the spool, cable, and weight into electric energy. At time 0, the weight begins to fall, the spool rotates, the cable unwinds, and electricity is generated. The hanging cable and the hanging weight are accelerated by gravity. The rotational moment of inertia of the spool, the torque from the electric generator, and the drag force act opposite to the gravitational force acting on the hanging weight. As cable leaves the spool, the spool's moment of inertia decreases (radius and mass decreases), and the hanging cable mass's gravitational force increases. Finally, the weight is raised by the motor/generator when surplus power from solar or wind sources are available.
Equations of Motion and 2nd Order Differential Equations
The equation of motion for the falling weight can be determined by summing the moments about the spool and the vertical forces about the weight. Recall that the sum of forces is equal to mass * acceleration, and the some of moments is equal to the rotational moment of inertia * angular acceleration.

At this point the two equations can be combined to solve for the linear acceleration of the weight. The step by step derivation is shown below. The final solution is also shown in the figure above, boxed in blue.

Last but not least... Relate the position, velocity, and acceleration with respect to time. That is, acceleration is the derivative of velocity which is the derivative of position.

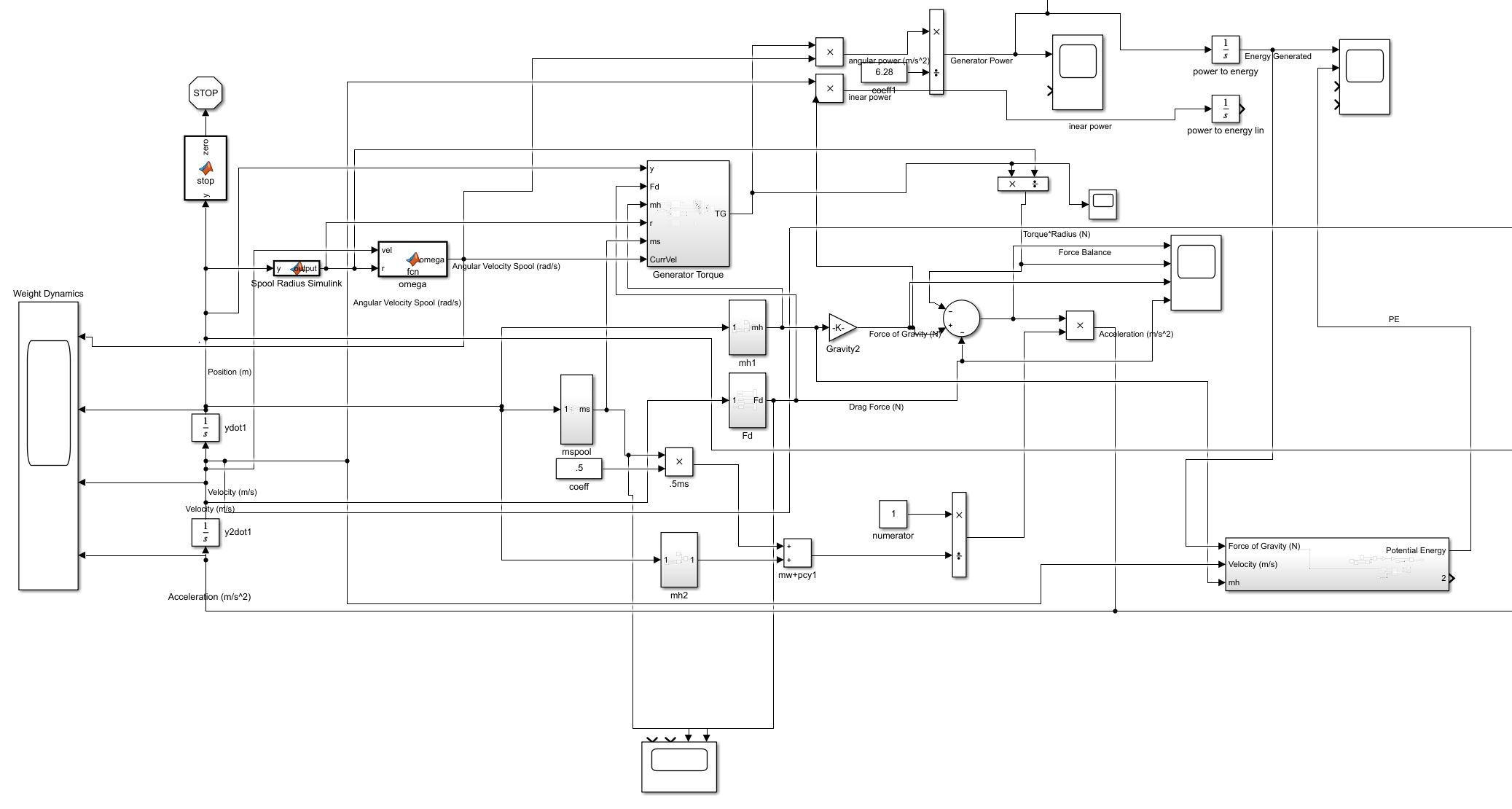
Simulation
The acceleration, velocity, position of the weight as well as the power generation of the generator can be solved numerically using MATLAB's built in ODE solver. I used MATLABs block diagram environment - simulink. It's a little messy, as I taught myself the program for this project.
Results
Check out my video for insights on the results! Discussion starts at the (18:30) mark with lots of cool graphs. The results ultimately helped us select our final concept and informed us on design improvements like generator sizing, cable and gearbox selection to improve longevity and increase profitability.
"I'm not a web developer nor have I been formally educated in web development, but I do enjoy building things, so here we are. I hope you enjoy my website." - Every Web Developer